Olá pessoal. Este vai ser o primeiro de uma série de posts em que vou falar sobre criptografia RSA. O RSA é o método de criptografia mais utilizado no mundo e o objetivo
desta série é mostrar a teoria matemática e a implementação dela em forma de algoritmo computacional. Atenção: ao acompanhar a série você vai descobrir que não existe mágica no processo e isto, as vezes, pode ser um pouco decepcionante.
Um pouco de história
Desde a antiguidade clássica, e talvez até antes, as pessoas usam criptografia para transmitir mensagens secretas. A idéia era simples: eu tenho um método ou chave que uso para “embaralhar” uma mensagem e só quem conhece este método ou mensagem conseguiria tornar esta mensagem legível novamente.
O grande problema desta abordagem é que tanto o emissor quanto o receptor tem que conhecer a chave da criptografia. Por exemplo, se eu – que estou em SP – quisesse mandar uma mensagem criptografada por mim para o pessoal da Lambda3 RJ agora, eu teria que arranjar uma forma segura de enviar para eles a chave que usei para cifrar o texto. Como eu poderia enviar esta chave de forma segura? Eu não conseguiria.
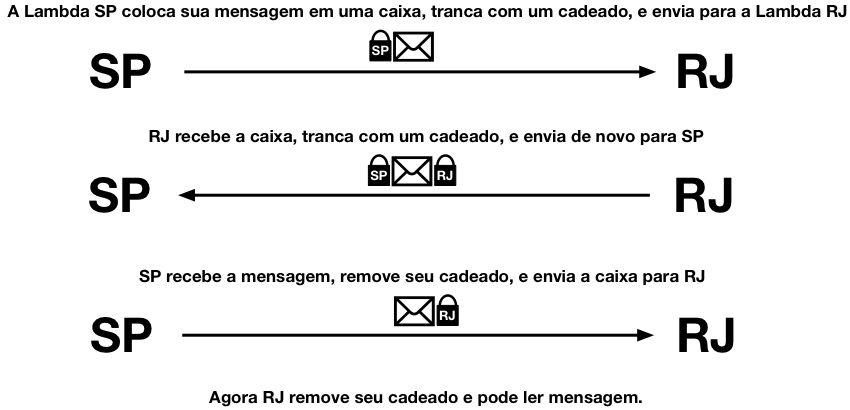
Esta abordagem é conhecida como criptografia de chave simétrica. Para solucionar o problema dela, começou-se a pensar em uma criptografia de chave assimétrica, ou seja, com duas ou mais chaves. Creio que o exemplo mais intuitivo disto seja o seguinte:
A vantagem desta abordagem é que não foi necessário que a Lambda 3 SP enviasse a sua chave para o RJ. O problema é que foram necessárias três viagens (!), e que não ciframos a mensagem em si, mas o “repositório” da mensagem.
Na década de 70 dois cientistas da computação que trabalhavam no MIT, Ronald Rivest e Adi Shamir, estavam empenhados em criar um método de criptografia de chave assimétrica eficiente. Eles foram ajudados pelo matemático Leonard Adleman, que validava as idéias dos dois pelo ponto de vista matemático. Em 1977 os três registraram a patente do método RSA.
E como o RSA funciona?
Esta é a parte legal. Com o RSA eu tenho duas chaves: uma pública e uma privada. A chave pública, como nome diz, eu posso distribuir livremente; qualquer pessoa pode usar a minha chave publica para criptografar uma mensagem para mim. Entretanto, só é possível descriptografar a mensagem usando a minha chave privada, que eu mantenho
em segredo.
Usando ainda a ideia do exemplo anterior, para a Lambda SP mandar uma mensagem para a Lambda RJ, basta que SP criptografe a mensagem com a chave pública da Lambda RJ e a envie. Somente o RJ conseguirá ler mensagem pois só eles tem a chave privada necessária para descriptografar a mensagem.
O RSA foi construído sobre uma das áreas mais clássicas da matemática, a Teoria dos números. Ele se baseia na dificuldade em fatorar um número em seus componentes primos. Primeiro vamos lembrar que um número primo é um número que só pode ser dividido por ele mesmo e por 1 (numa divisão exata, sem números quebrados); segundo, temos que lembrar como descobrir os fatores primos de um número.
Segundo o Teorema Fundamental da Aritmética todo número inteiro positivo maior que 1 pode ser decomposto de forma única em um produto de números primos, por exemplo:
26 = 2 * 13 44 = 2 * 2 * 11
Fatorar números pequenos é algo simples, mas fatorar números grandes é bem difícil e demorado, pois este é um problema que não pode ser resolvido em um tempo polinomial determinístico, ou falando de forma bem simplificada, não há uma fórmula para isto.
E como o RSA usa isto tudo? As chaves pública e privada são geradas com base na multiplicação de dois números primos. O resultado desta multiplicação será público mas, se o número for grande o suficiente, fatorar este número para descobrir os primos que multiplicamos para formá-lo pode demorar anos.
É desta particularidade que vem segurança do RSA. Na verdade não é impossível quebrar a criptografia RSA, mas como para fazer isto seriam necessários alguns bons anos ou décadas, a ideia se torna inviável.
Preparem papel, caneta e calculadora pois no próximo post vamos executar o passo-a-passo do método e criptografar/descriptografar algumas mensagens. Até mais!
Fernando Oliveira
Programador cabeludo que gosta de matemática, filmes B e cerveja - e é aficionado por festas juninas.