Há oito anos, o Giovanni Bassi falou sobre inferência de tipos em F#. O exemplo que ele deu envolvia a soma dos quadrados dado um array. Como o objetivo era mostrar como funcionava a inferência de tipos, a abordagem imperativa foi suficiente. Mas ele fez uma nota ao final do artigo:

(…) eu só queria dizer que essa não é a maneira correta de fazer uma função com F#. Programar F# assim é como usar C# para fazer programação estruturada, sem OO, algo que devia dar cadeia. Esse programa, altamente imperativo, vai contra tudo o que o F# propõe, que é uma programação funcional, não imperativa.

Então, qual seria a implementação funcional? E mais importante, como podemos partir da abordagem imperativa para a abordagem funcional de modo progressivo?

A implementação imperativa

A implementação do post sobre inferências é um bom ponto de partida:

let quadrado x = x * x

let somaDosQuadrados nums = 
    let mutable total = 0.0
    for x in nums do
      total <- total + quadrado x
    total
    
printfn "Resultado: %A" (somaDosQuadrados [|1.0; 2.0; 3.0|])
// Resultado: 14.0

Essa abordagem imperativa é bem próxima ao que faríamos em linguagens imperativas como C# ou javascript, por exemplo:

function quadrado(x) {
  return x * x;
}

function somaDosQuadrados(nums) {
  let total = 0;
  for (let i = 0; i < nums.length; i++) {
    total += quadrado(nums[i]);
  }
  return total;
}
console.log("Resultado: %d", somaDosQuadrados([1,2,3])) 
// Resultado 14

A implementação funcional

A principal mudança no mindset funcional é pensar em o que é ao invés de como fazer. Isso signigica que devemos definir o que é a soma dos quadrados, em vez de nos concentrarmos em como calcular. O quadrado de um número já está bem definido x = x * x. Mas o que é a soma dos valores de um array?

A soma dos valores de um array não é nada mais que o valor do primeiro elemento mais a soma dos valores restantes, certo?

let rec soma nums = (Array.head nums) + (soma (Array.tail nums))

Array.head retornará o primeiro elemento de um array, enquanto Array.tail retornará o restante do array. Essa função define bem a soma de um array, mas o que acontece quando o array não possuir mais elementos?

Um erro informando que o array está vazio!

Então devemos verificar se o array está vazio antes de realizarmos a operação de soma.

Condição de parada

Qual é o valor que devemos retornar quando o array está vazio? Para facilitar a vizualização podemos fazer um teste de mesa da função soma recursiva para os valores [|1;2;3|].

soma([1;2;3]) <=>
  1 + soma([2;3]) <=>
  1 + 2 + soma([3]) <=>
  1 + 2 + 3 + soma([])  <=>
  4 + soma([])

Por qual valor você substituiria soma([]) para que a expressão 4 + soma([]) seja igual a 4? Isso mesmo, zero!

A condição para verificarmos se o array está vazio é chamado de critério de parada da recursão. Ela é responsável por parar a árvore de chamadas da função recursiva. A implementação da soma, agora considerando array vazio será:

let rec soma nums = 
   if Array.length nums = 0 then 0
   else Array.head nums + soma (Array.tail nums)

Agora temos uma função que soma os valores de um array corretamente! soma [|1;2;3|] retornará corretamente 6.

Porém, pelo teste de mesa acima é possível perceber que essa solução não escala, pois para um array que contenha muitos valores a árvore de chamadas será enorme. Como a soma acumulada está implícita em cada chamada de recursão, o compilador não conseguirá otimizar a função.

Recursão em cauda

Para que o compilador consiga otimizar a função, basta movermos a informação do acumulador que está implícita na chamada da função para um parâmetro explícito. Isso fará com que as chamadas de funções sejam otimizáveis, pois não será mais necessário guardar uma informação na stack trace (de fato, algoritmos recursivos em cauda serão compilados como se fossem instruções de laço for).

let rec soma acc nums = 
  if Array.length nums = 0 then acc
  else 
    let novoAcc = acc + (Array.head nums)
    soma novoAcc (Array.tail nums)

Perceba que agora temos um parâmetro a mais chamado acc. Esse parâmetro contém a informação do acumulador até o momento da chamada da função. Um teste de mesa análogo acima seria:

soma 0 ([1;2;3]) <=>
  soma 1 ([2;3]) <=>
  soma (1+2) ([3]) <=> soma 3 ([3])
  soma (3+3) ([])  <=> soma 6 ([])
  6

Pelo teste de mesa é fácil ver que cada chamada recursiva não contém mais informações na stack trace.

Porém um problema nessa abordagem é que um acumulador inicial deverá ser fornecido para que a soma seja realizada (soma 0 [|1;2;3|]), mas poderemos resolver isso facilmente com uma função local:

let soma nums =     
    let rec somaRec acc nums = 
      if Array.length nums = 0 then acc
      else 
        let novoAcc = acc + (Array.head nums)
        somaRec  novoAcc (Array.tail nums)
    somaRec 0 nums

somaRec é uma função local de soma, que é apenas uma casca para facilitar a chamada da soma recursiva.

Agora temos uma função que soma valores de um array de forma performática e seguindo uma abordagem funcional. Mas a solução ficou um tanto quanto verbosa e não parece mais declarativa que a implementação imperativa.

Será que conseguimos melhorar?

Pattern matching

Não vou ser extensivo sobre esse tópico pois ele merece um post à parte, por hora podemos entender pattern matching como um mecanismo para identificarmos valores pelo formato dos dados.

Podemos identificar uma lista como vazia utilizando [] ou através do operador cons onde cada :: separa um elemento da lista restante. Por exemplo em x::xs, x representa o primeiro elemento do lista, enquanto xs representa o restante. Logo nossa implementação de soma poderá ser refatorada da seguinte forma:

let rec somaRec acc nums = 
  match nums with
  | [] -> acc
  | x::xs -> somaRec (x + acc) xs

Agora sim! Temos a implementação da soma de forma mais declarativa!

Mas e a função quadrado? Onde ela se encaixa? Poderíamos aplica-lo antes de somar ao acumulador (ex: x::xs -> somaRec (quadrado(x) + acc) xs), mas aí não poderíamos aproveitar mais a função soma para apenas somar elementos de um array.

Será que não temos outra solução?

Transformaçao

Outro valor muito importante para uma abordagem mais funcional é a transformação. A soma dos quadrados de um array nada mais é do que a aplicação de sucessivas transformações ao array original. Podemos transformar o array em uma lista de valores elevados ao quadrado, depois é só somar eles.

Partindo da função soma acima, podemos trocar a função de soma pela função quadrado e o acumulador por uma lista. Assim teríamos uma função que eleva ao quadrado os valores de um array.

let rec mapRec acc nums = 
  match nums with
  | [] -> acc
  | x::xs -> mapRec (quadrado(x)::acc) xs

Podemos tornar essa função genérica facilmente se em vez de quadrado a função de transformação fosse informada como um parâmetro:

let rec mapRec f acc nums = 
  match nums with
  | [] -> acc
  | x::xs -> mapRec (f(x)::acc) xs

Agora temos uma função de transformação genérica! Podemos finalmente escrever a soma dos quadrados da seguinte maneira:

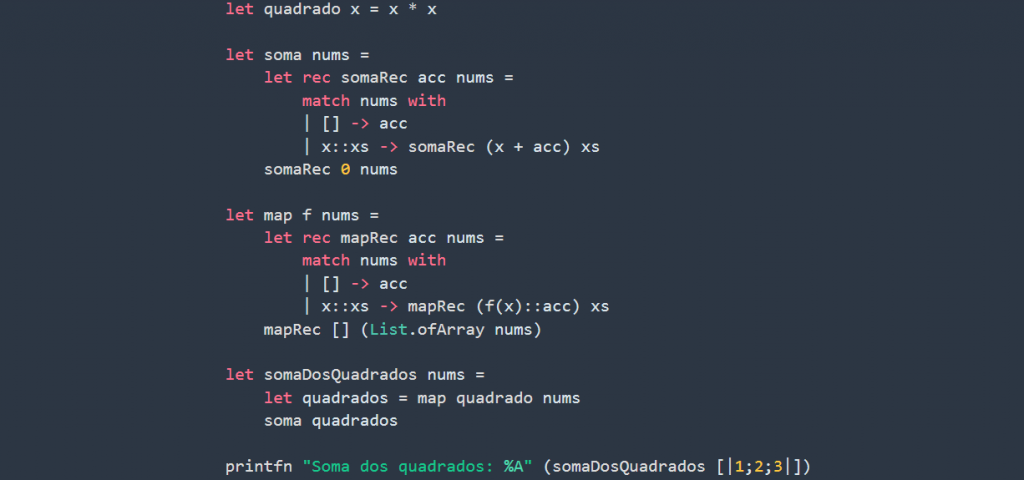
let quadrado x = x * x

let soma nums =     
    let rec somaRec acc nums = 
      match nums with
      | [] -> acc
      | x::xs -> somaRec (x + acc) xs
    somaRec 0 nums

let map f nums = 
    let rec mapRec acc nums = 
      match nums with
      | [] -> acc
      | x::xs -> mapRec (f(x)::acc) xs
    mapRec [] (List.ofArray nums)

let somaDosQuadrados nums =
    let quadrados = map quadrado nums
    soma quadrados

printfn "Soma dos quadrados: %A" (somaDosQuadrados [|1;2;3|])
// Soma dos quadrados: 14

Pronto! Agora temos uma função que está alinhada com conceitos funcionais e calcula a soma dos quadrados.

Mas, transformações e somas em listas parecem problemas comuns. Será que já não existe uma implementação padrão?

Implementação funcional final

Como dito neste post, o processamento de listas é algo natural e muito mais fácil de se fazer em linguagens funcionais.

Para somarmos os valores de um array basta chamar Array.sum. Para aplicar transformações basta chamarmos Array.map. A implementação final ficará assim:

let quadrado x = x * x

let somaDosQuadrados nums = 
    Array.map quadrado nums |> Array.sum

printfn "Soma dos quadrados: %A" (somaDosQuadrados [|1;2;3|])
// Soma dos quadrados: 14

Peço desculpas, pois provavelmente é neste momento que você está bravo e inconformado comigo e não entende porque então passamos por todas essas implementações e conceitos teóricos.

O objetivo principal deste artigo não foi mostrar como é a implementação funcional, mas sim como pensar funcional. Espero que a essa altura, eu tenha conseguido mostrar um pouco mais do pensamento funcional.

Portanto, não se preocupe caso não tenha entendido alguma construção da linguagem. O importante é que você entenda os conceitos que guiam uma abordagem mais funcional.

Bônus: implementação funcional em linguagens imperativas

Você pode argumentar que em javascript ou C# podemos utilizar construções como map, reduce, high order functions ou até mesmo o linq.

Todas essas construções são baseadas em conceitos funcionais, e como gostaria de comparar uma implementação puramente funcional com uma implementação puramente imperativa, o uso dessas ferramentas injustiçaria a comparação.

Mas uma implementação funcional equivalente em javascript seria:

const quadrado = x => x * x

const somaDosQuadrados = nums =>
  nums.map(quadrado).reduce((x,y) => x+y, 0)

Percebe a forte influência das linguagens funcionais? Essa implementação em Javascript é bem parecida com a nossa implementação final em F#.

Aprender linguagem funcional provavelmente irá influenciar seu código, mesmo em uma linguagem imperativa.

[box type=”shadow”]

[/box]

Conclusão

Partimos de uma implementação totalmente imperativa para uma implementação totalmente funcional progressivamente.

Quando compararmos as duas soluções finais, fica evidente o ganho de declaratividade e a quantidade reduzida de linhas na abordagem funcional.
Para o mindset funcional é importante perceber que

• procuramos definir o que as coisas são, não como fazer e
• conduzimos transformações sucessivas para chegar ao resultado desejado

Espero que esse artigo tenha lhe dado um insight sobre como pensar de modo funcional para alguns problemas que podemos enfrentar no dia a dia.

Um abraço,
Francisco

(Cross-post de https://chicocode.io/pt-br/posts/revisitando-soma-dos-quadrados/)